机器学习(Machine Learning, ML)是人工智能(Artificial Intelligence, AI)的一个重要的分支,机器学习算法是一类从数据中自动分析获得规律,并利用规律对未知数据进行预测的算法。K-NN(K Nearest Neighbor)算法是机器学习中最基础也是最简单的算法之一,下面我们就来了解一下这个算法是怎么工作以及是怎么帮助我们解决问题的。
1. kNN算法的原理
kNN算法的原理极其简单,即首先存在一个训练样本数据集,且训练集中的每一个数据都会存在一些特征,并且该数据会拥有一个已知的分类。在输入未知分类的测试数据的时候,根据它的特征内容将测试数据和每一条训练数据进行比较,然后提取出训练数据中与测试数据最相似的k个数据(这就是kNN算法名称的来历),然后取出这个k个数据中出现次数最多的分类,作为测试数据的分类。
2. 如何通过特征来比较训练数据和测试数据的相似度
通过特征值来计算相似度需要用到一点点的数学内容,如果训练数据称为A,测试数据为B,这个数据共有1, 2, …, n个特征,则它们的相似度可以使用如下公式表示:
方法很简单,就是取它们的特征之差的平方和,之后开平方得到x,x越小则说明这两个数据在当前特征下越相似。
但是,不同的数据之间可能存在数值上的差异。例如,对于一个上市公司,其营业额是必然大于其员工数的,那么此时把营业额的差值和员工数的差值同等对待显然是不合适的。利用下面的公式可以把任意取值范围的特征值转化到0到1区间之内的值:
其中min和max分别为数据集中的最小特征值和最大特征值。接下来,只需要使用newValue作为新的特征值就可以了,虽然这样增加了计算量,不过我们必须这样做。至此我们已经知道了kNN算法的基本工作方式,下面我们通过一个实际的例子来了解一下KNN算法是如何工作的。
3. kNN算法实现数字识别
想要通过kNN算法实现数字识别,首先我们需要提供大量已知数字值的训练数据,之后把测试数据扔到任务中去与训练数据比对,最终分析出该数字的可能值。
这里存放了一些训练数据,每一个文件都对应一个数字,并且数字的真实值在文件名中表示了出来。测试数据也同样的是一个文件对应一个数字,我们的任务就是把测试数据文件中的数字值给识别出来。
下面我们使用Python来实现kNN算法(需要安装numpy模块),程序主要就分为这几步:
- 读入训练数据构造为一个矩阵,把训练文件的字符串通过取出每一行然后首尾相连的方式构造为一个字符数组,每一个训练数组都作为矩阵的一行;
- 通过同样的方式把测试数据构造为一个只有一行的矩阵;
- 把测试数据同每一条训练数据做比较,选出差异最小的k条训练数据;
- 把k条数据中所占比例最大的数字作为测试数字的识别结果;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
|
import operator
from os import listdir
from numpy import zeros, tile
TRAINING_PATH = 'digits/trainingDigits/'
TRAINING_REAL_NUMS = []
TEST_PATH = 'digits/testDigits/'
TEST_REAL_NUMS = []
def _make_matrix_by_file(file):
"""
把指定文件内的数据生成一个一维矩阵
:param file:
:return:
"""
file_data_array = zeros((1, 1024))
with open(file) as lines:
for line_num, line in enumerate(lines):
for i in range(32):
file_data_array[0, 32 * line_num + i] = int(line[i])
return file_data_array
def generate_training_matrix():
"""
读取所有训练文件的数据并且转化为一个矩阵
:return:
"""
training_file_list = listdir(TRAINING_PATH)
training_matrix = zeros((len(training_file_list), 1024))
for file_index, training_file in enumerate(training_file_list):
TRAINING_REAL_NUMS.append(training_file.split('.')[0].split('_')[0])
training_matrix[file_index, :] = _make_matrix_by_file(TRAINING_PATH + training_file)
return training_matrix
def generate_test_matrix_list():
"""
读取所有测试文件的数据并且转化为一个矩阵list
:return:
"""
test_file_list = listdir(TEST_PATH)
test_matrix1_list = []
for test_file in test_file_list:
TEST_REAL_NUMS.append(test_file.split('.')[0].split('_')[0])
test_matrix1_list.append(_make_matrix_by_file(TEST_PATH + test_file))
return test_matrix1_list
def classify(training_matrix, test_matrix, k=3):
"""
通过训练矩阵对测试数据进行数字判断
:param training_matrix: 完整的训练矩阵
:param test_matrix: 测试数据
:param k: 取最相似的k个训练数据
:return: 分类结果
"""
training_matrix_lines = training_matrix.shape[0]
test_matrix = tile(test_matrix, (training_matrix_lines, 1))
distances = (((test_matrix - training_matrix) ** 2).sum(axis=1)) ** 0.5
sorted_distances_index = distances.argsort()
num_count = {}
for i in range(k):
one_possible_number = TRAINING_REAL_NUMS[sorted_distances_index[i]]
num_count[one_possible_number] = num_count.get(one_possible_number, 0) + 1
sorted_num_count = sorted(num_count.items(), key=operator.itemgetter(1), reverse=True)
return sorted_num_count[0][0]
def run():
training_matrix = generate_training_matrix()
test_matrix_list = generate_test_matrix_list()
right = 0
total = 0
for idx, test_matrix in enumerate(test_matrix_list):
real = TEST_REAL_NUMS[idx]
guess = classify(training_matrix, test_matrix, 3)
if real == guess:
right += 1
total += 1
print('real: ', real, ', guess: ', guess)
fail = total - right
print(fail, ' fails, fail rate is ', fail / total)
if __name__ == '__main__':
run()
|
上述代码的主要流程和操作已经在注释中做了比较详细的介绍,可能只有第67行的矩阵运算需要略作介绍,下面使用一个例子来介绍这里是怎么运算的。首先我们在66行中已经构造了一个和训练数据矩阵行数和列数都一样的测试数据矩阵,之后我们发现第67行一共做了如下几个操作:
- 两个矩阵相减;
- 求矩阵平方(即矩阵相乘);
- 对矩阵进行行求和;
- 对矩阵进行开方操作;
我们先构造两个如下的矩阵:
a = array([[2, 3, 4, 5],
[3, 4, 5, 6],
[4, 5, 6, 7]])
b = array([[3, 4, 5, 6],
[0, 0, 0, 0],
[9, 8, 7, 6]])
之后两个矩阵相减,得到如下结果,可见相减是矩阵中每个对应位置的元素都做了减法操作
array([[-1, -1, -1, -1],
[ 3, 4, 5, 6],
[-5, -3, -1, 1]])
之后再对上面得到的矩阵做平方,也就是自己乘以自己,实际上是对每个对应位置的元素都做了乘法操作,平方结果如下
array([[ 1, 1, 1, 1],
[ 9, 16, 25, 36],
[25, 9, 1, 1]])
之后对矩阵的每一行求和,使用方法 matrix.sum(axis=1) 可以简单做到,行求和后结果如下
array([ 4, 86, 36])
最后再做一次开方,实际上就是对矩阵中的每个元素做开方,结果如下
array([ 2. , 9.2736185, 6. ])
下面是我在IPython中的操作过程
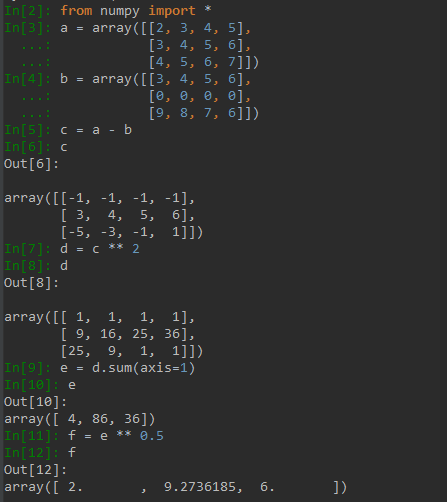
完整的代码和数据可以从这里获取到。
本文链接: https://www.nosuchfield.com/2017/05/26/K-Nearest-Neighbor-Algorithm-for-Digital-Recognition/
